益智游戏克星:BFS暴力搜索算法
益智游戏克星:BFS暴力搜索算法
滑动拼图游戏大家应该都玩过,下图是一个 4x4 的滑动拼图:

拼图中有一个格子是空的,可以利用这个空着的格子移动其他数字。你需要通过移动这些数字,得到某个特定排列顺序,这样就算赢了。
我小时候还玩过一款叫做「华容道」的益智游戏,也和滑动拼图比较类似:

那么这种游戏怎么玩呢?我记得是有一些套路的,类似于魔方还原公式。但是我们今天不来研究让人头秃的技巧,这些益智游戏通通可以用暴力搜索算法解决,所以今天我们就学以致用,用 BFS 算法框架来秒杀这些游戏。
一、题目解析
LeetCode 第 773 题就是滑动拼图问题,题目的意思如下:
给你一个 2x3 的滑动拼图,用一个 2x3 的数组board表示。拼图中有数字 0~5 六个数,其中数字 0 就表示那个空着的格子,你可以移动其中的数字,当board变为[[1,2,3],[4,5,0]]时,赢得游戏。
请你写一个算法,计算赢得游戏需要的最少移动次数,如果不能赢得游戏,返回 -1。
比如说输入的二维数组board = [[4,1,2],[5,0,3]],算法应该返回 5:
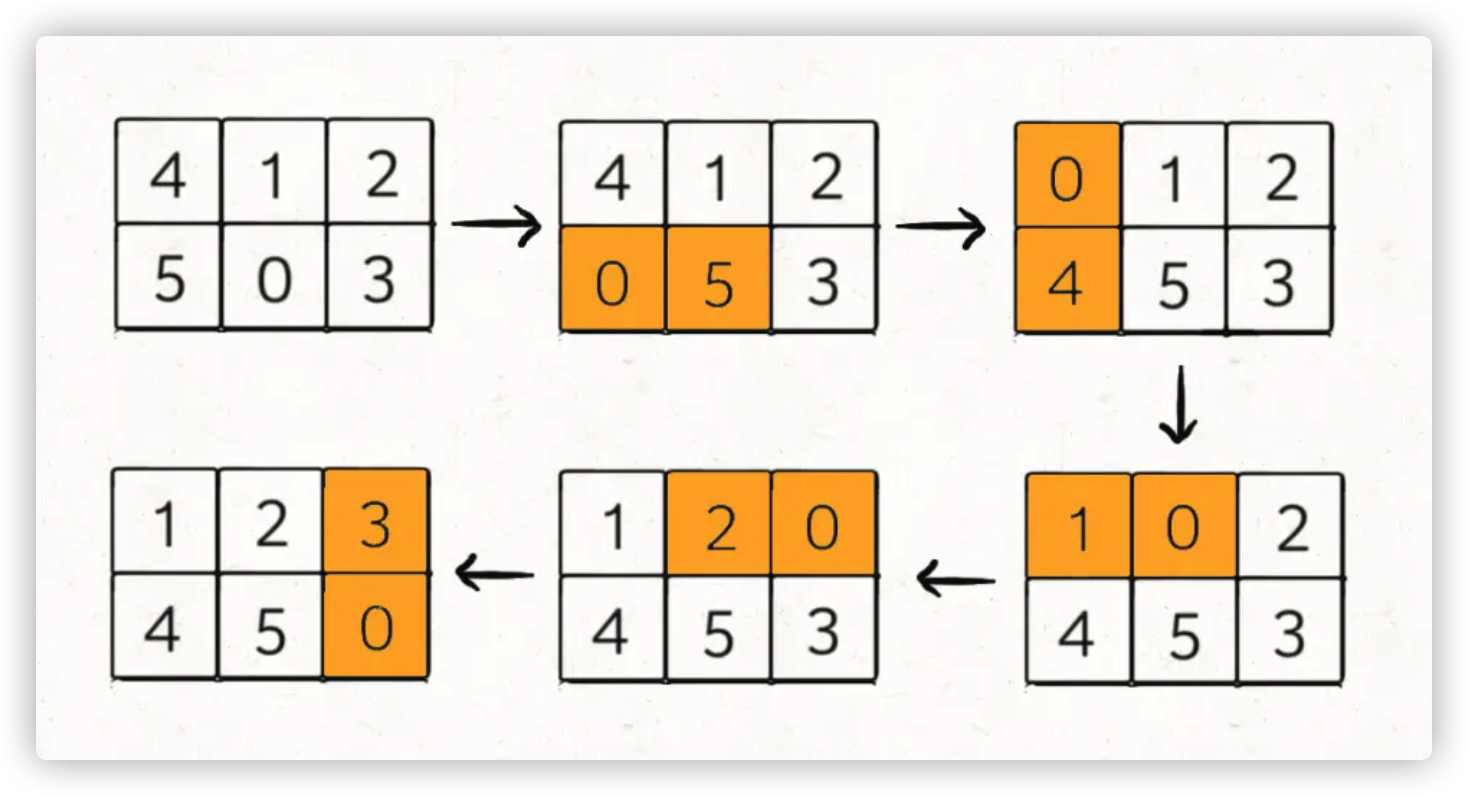
如果输入的是board = [[1,2,3],[4,0,5]],则算法返回 -1,因为这种局面下无论如何都不能赢得游戏。
二、思路分析
对于这种计算最小步数的问题,我们就要敏感地想到 BFS 算法。
这个题目转化成 BFS 问题是有一些技巧的,我们面临如下问题:
1、一般的 BFS 算法,是从一个起点start开始,向终点target进行寻路,但是拼图问题不是在寻路,而是在不断交换数字,这应该怎么转化成 BFS 算法问题呢?
2、即便这个问题能够转化成 BFS 问题,如何处理起点start和终点target?它们都是数组哎,把数组放进队列,套 BFS 框架,想想就比较麻烦且低效。
首先回答第一个问题,BFS 算法并不只是一个寻路算法,而是一种暴力搜索算法,只要涉及暴力穷举的问题,BFS 就可以用,而且可以最快地找到答案。
你想想计算机怎么解决问题的?哪有那么多奇技淫巧,本质上就是把所有可行解暴力穷举出来,然后从中找到一个最优解罢了。
明白了这个道理,我们的问题就转化成了:如何穷举出board当前局面下可能衍生出的所有局面?这就简单了,看数字 0 的位置呗,和上下左右的数字进行交换就行了:
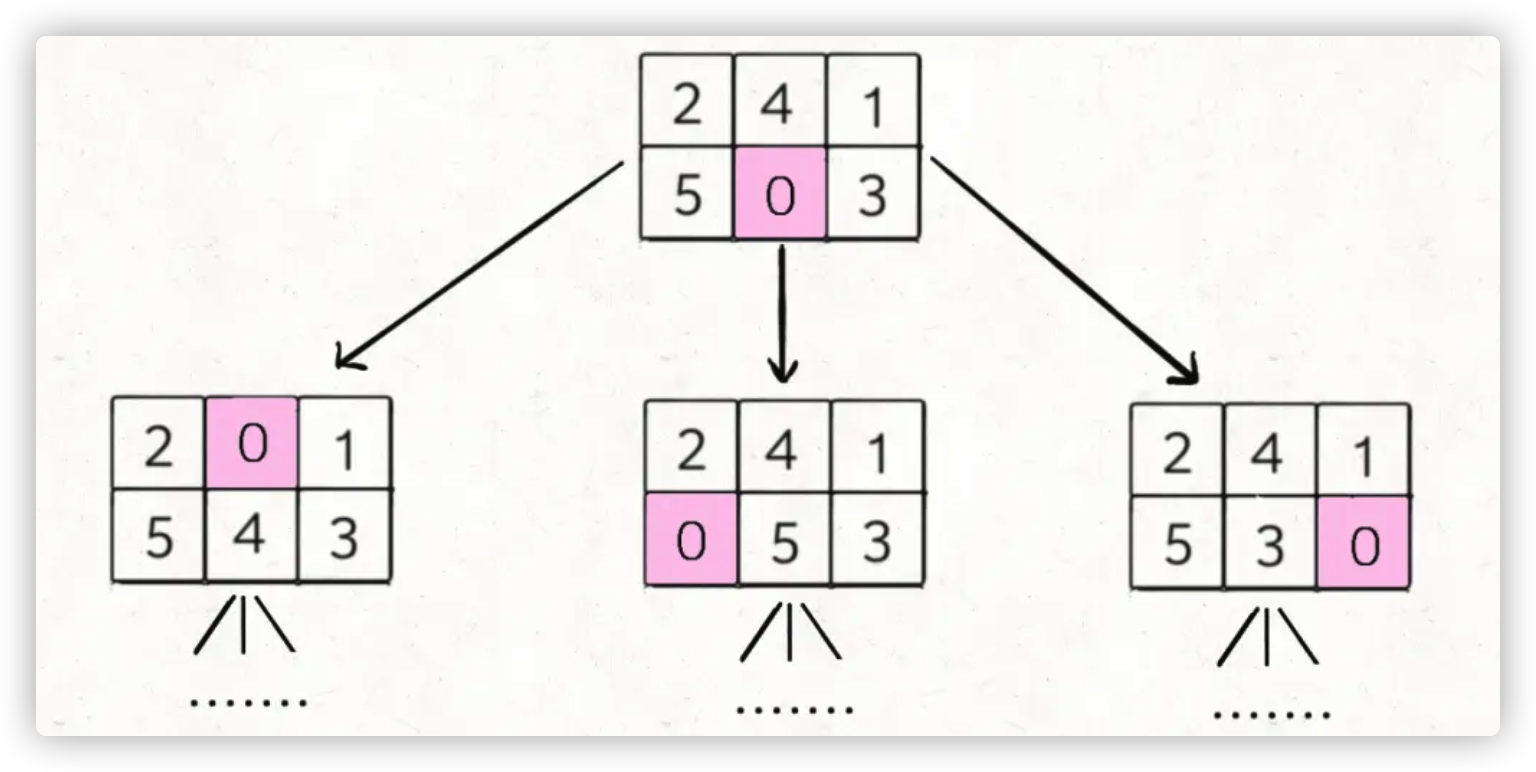
这样其实就是一个 BFS 问题,每次先找到数字 0,然后和周围的数字进行交换,形成新的局面加入队列…… 当第一次到达target时,就得到了赢得游戏的最少步数。
对于第二个问题,我们这里的board仅仅是 2x3 的二维数组,所以可以压缩成一个一维字符串。其中比较有技巧性的点在于,二维数组有「上下左右」的概念,压缩成一维后,如何得到某一个索引上下左右的索引?
很简单,我们只要手动写出来这个映射就行了:
vector<vector<int>> neighbor = {
{ 1, 3 },
{ 0, 4, 2 },
{ 1, 5 },
{ 0, 4 },
{ 3, 1, 5 },
{ 4, 2 }
};
这个含义就是,在一维字符串中,索引i在二维数组中的的相邻索引为neighbor[i],:
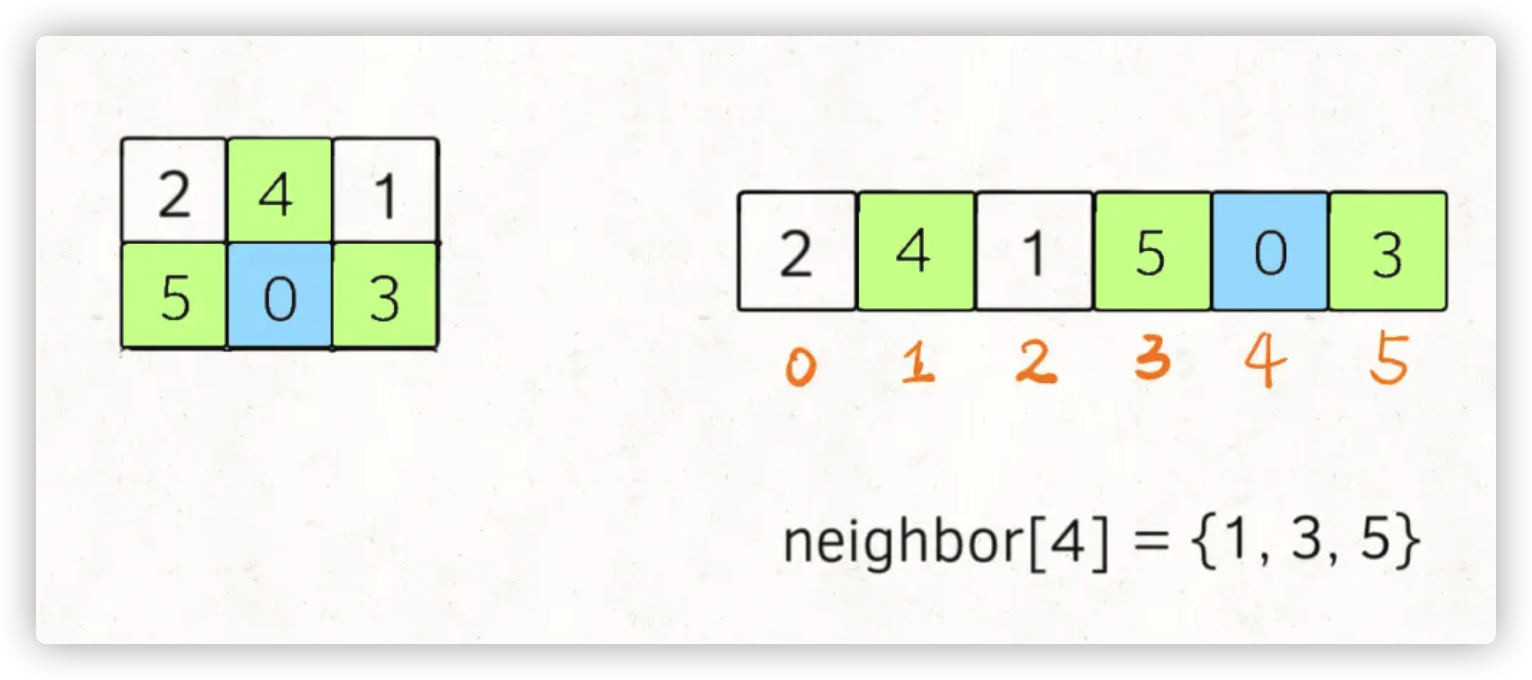
至此,我们就把这个问题完全转化成标准的 BFS 问题了,借助前文 BFS 算法框架套路详解 的代码框架,直接就可以套出解法代码了:
int slidingPuzzle(vector<vector<int>>& board) {
int m = 2, n = 3;
string start = "";
string target = "123450";
// 将 2x3 的数组转化成字符串
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
start.push_back(board[i][j] + '0');
}
}
// 记录一维字符串的相邻索引
vector<vector<int>> neighbor = {
{ 1, 3 },
{ 0, 4, 2 },
{ 1, 5 },
{ 0, 4 },
{ 3, 1, 5 },
{ 4, 2 }
};
/******* BFS 算法框架开始 *******/
queue<string> q;
unordered_set<string> visited;
q.push(start);
visited.insert(start);
int step = 0;
while (!q.empty()) {
int sz = q.size();
for (int i = 0; i < sz; i++) {
string cur = q.front(); q.pop();
// 判断是否达到目标局面
if (target == cur) {
return step;
}
// 找到数字 0 的索引
int idx = 0;
for (; cur[idx] != '0'; idx++);
// 将数字 0 和相邻的数字交换位置
for (int adj : neighbor[idx]) {
string new_board = cur;
swap(new_board[adj], new_board[idx]);
// 防止走回头路
if (!visited.count(new_board)) {
q.push(new_board);
visited.insert(new_board);
}
}
}
step++;
}
return -1;
/******* BFS 算法框架结束 *******/
}
至此,这道题目就解决了,其实框架完全没有变,套路都是一样的,我们只是花了比较多的时间将滑动拼图游戏转化成 BFS 算法。
很多益智游戏都是这样,虽然看起来特别巧妙,但都架不住暴力穷举,常用的算法就是回溯算法或者 BFS 算法,感兴趣的话我们以后再聊。