Java中float和double中溢值问题和浮点数的储存问题
记录一下初学Java出现的问题。
以为之前是从Python起步的,最初了解到Java的数据类型有float和double这两个东西,就尝试相加这两个
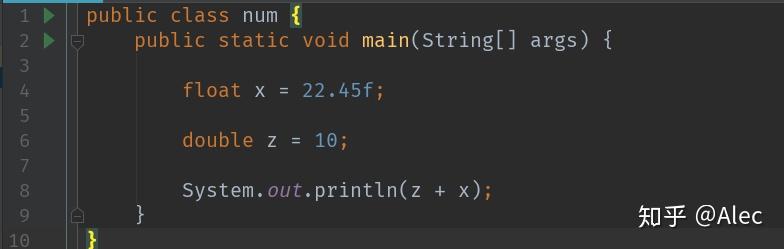
这里返回的结果:32.45000076293945
这个返回值看的我一脸懵
要理解这个问题要先知道浮点数在计算机中是以什么形式储存的
首先要知道计算机能懂的只有0和1
每一个0和1都占一个位 bit (比特)(Binary Digits):存放一位二进制数,最小的存储单位。
所以,整数部分:
22 / 2 = 11 余0
11 / 2 = 5 余1
5 / 2 = 2 余1
2 / 2 = 1 余0
1 / 2 = 0 余1
22的二进制转换就是10110
小数部分:
0.45 * 2 = 0.9 0
0.9 * 2 = 1.8 1
0.8 * 2 = 1.6 1
0.6 * 2 = 1.2 1
0.2 * 2 = 0.4 0
0.4 * 2 = 0.8 0
0.8 * 2 = 1.6 1
0.6 * 2 = 1.2 1
0.2 * 2 = 0.4 0
……
我们可以发现0.45转化成二进制的时候是无限循环的
二进制转换完成,22.45 –> 10110.011100110……
得到这个二进制浮点数之后,计算机是怎么把他表示为没有小数点的字符呢?
就要用到小学学过的科学记数法:
10110.011100110可以写为
1.0110011100110
过程中我们发现,小数的转换有可能会产生无限循环的情况,想要做的最精确的记录22.45,计算机需要无限大的空间来记录
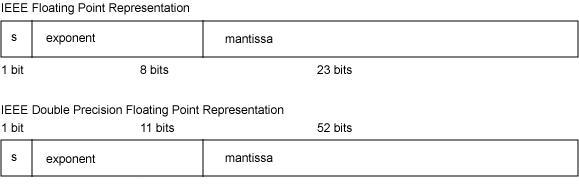
那么IEEE754标准就规定:
32位单精度(java中的float),使用32位(bit)来存储
64位双精度(double), 使用64位储存
那采用什么样的格式呢
|S| Exp | Fraction |
+-+——–+———————–+
S:符号位(正0负1)
EXP:指数位
Fraction:有效数字
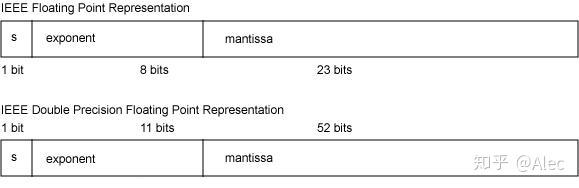
单精度(float)就是
|1(bit)| 8(bit) | 23(bit) |
+-+——–+———————–+
双精度(double)
|1(bit)| 11(bit) | 52(bit) |
+-+——–+———————–+
以22.45为例:
1.0110011100110
(二进制科学记数)
S = 0
EXP = 4+127 =131 –> 10000011
这里为什么是131而不是直接的4呢?
0000 0000八个位来表示指数,最大值就是1111 1111 –> 十进制就是 255
指数会有正负数两种情况,所以分两半,255 / 2 = 127.5
0~127用于负数
127~255用于正数
127相当于一个指数是0,所以表示正指数就 + 同理 -
Fraction = 0110011100110(这里只有13(bit))
= 01100111001100110011010(接着算了10(bit)补齐23(bit))
所以22.45在计算机里就是 S+EXP+Fraction = 01000001101100111001100110011010
同理**双精度(double)**有64位来记录

System.out.println(Integer.toBinaryString(Float.floatToIntBits(x)));
这行代码可以查看22.45的二进位表达
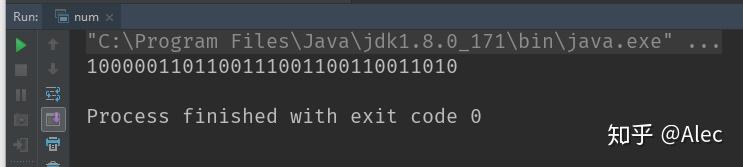
为什么没有0,因为01 跟1是一样的,所以0就不会显示了
这是-22.45

=======================================================
了解了IEEE二进位浮点数,知道了float和double记录的浮点精确度不一样我们再看一下问题。
从输出的结果看 32.45000076293945 是一个double类型,精确的表示了小数点后14位
所以float + double 是从float赋值到double

输出结果:22.450000762939453
可是如果float(单精度)赋值到double(双精度)出现精度丢失可以理解,但是会什么会溢值呢?
我们可以从二进制推回十进制来看一看
0 | 10000011 | 01100111001100110011010
正| 指数=4 |有效数字
1.01100111001100110011010
= 10110.0111001100110011010
后面这个0.0111001100110011010表示小数位
我们可以通过把0.0111001100110011010换成十进制来看看
小数的二进制到十进制的方法是
从小数点后依次乘以2的负一次方,2的负二次方,2的负三次方等
0.0111001100110011010
可以直接用python一算

同这个结果,我们可以看出,由于float单精度只能选取 无限循环的二进制小数的23位
导致了十进制浮点数在存储时的不够精准
当我们把已经储存好的32二进制格式转换成64位时
输出结果:

可以看出Java并没有重新计算小数点后的更多位, 而是用0来补位
所以转换成double后,之前float没有精确到的位数就会显示出来。
要解决这个问题就需要使用java.math中提供的API类BigDecimal
注:(BigDecimal用String 或Integer 初始化,double初始化会有舍入精度问题)